An analogy can be used to better describe the concept of time constant. Consider a bucket full of water elevated to some height, say h. This height is equivalent to the voltage V on our capacitor.

We can consider a big bucket (with big diameter) with water at height h as having a certain capacity, equivalent to the energy stored by our capacitor whose capacitance is C. A smaller bucket (with smaller diameter) with water still at height h will have a smaller capacity. The energy stored in our capacitor is equal to

E =1/2 CV 2

If the bucket has a hole in it, then it will leak and the water level will decrease from height h to zero. If the hole is big, then the leak will be quick. If the hole is small then the leak will be slow. The bigger the hole, the smaller the resistance R of our capacitor. The smaller the hole, the bigger the R. Thus the smaller the R, the quicker the voltage drop and hence the energy decrease.

If we have a bigger capacity bucket (proportional to our capacitance C), but the height h is as before, then it will take longer for the height to decrease to zero, given a constant sized hole. Thus the smaller the C, the quicker the voltage drop and hence the energy decrease.

The rate at which the height (voltage) decreases depends on the product of R and C and is called a time constant, and it is normally given a symbol t.

t = RC

Figure A shows how the voltage of a capacitor drops from an initial voltage of 3.0 V with a time constant t of 1 second. The shape of this graph does not change. If the time constant doubles, then the scale doubles.

Figure A: Time Constant of 1 second

     

 

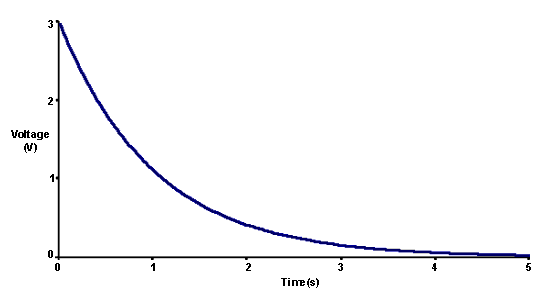
Within a period of one time constant, t, the voltage has dropped to 1/3 of its initial value. Therefore the energy has dropped to 1/9 of its initial value, 89% of the capacitor's energy has been used and 11 % is still stored in the capacitor. Conventionally, a capacitor is discharged to 1/2 of its initial voltage, retaining 1/4 of its initial energy, thereby utilising 75%.

This raises the question of efficiency. The implication of the above statement is that there is no energy wasted. This is not true. Energy is wasted in the resistor (it becomes heat, and thus heats the capacitor). How much energy is wasted in the capacitor and how much is delivered to the load (the place the energy is needed) thus depends on the ratio of the resistance of the capacitor, R, to the resistance of the load. The smaller the R, the less the loss and the greater the efficiency.

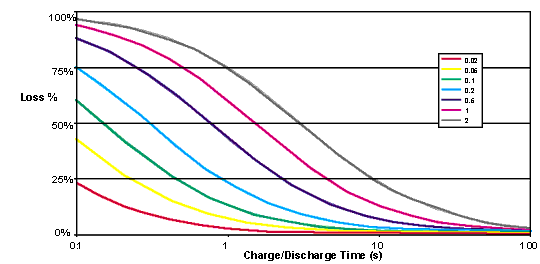
If it is desired to discharge the capacitor to half of its initial voltage, thereby utilising 75% of the stored energy, then the energy lost on discharge can be determined for different discharge times. If you discharge slowly, then the resistance of the load must be quite high, so that the resistance R can be relatively small. Thus as discharge gets faster, the resistance R becomes more important, generating losses. For very fast discharges, there are very high losses. However, as the time constant t decreases, so does R, and hence losses become smaller. This effect is shown in Figure B.

Figure B: Losses for RC time constants from 0.02 to 2 seconds

 

CAP-XX produces supercapacitors with time constants from 0.001 seconds to 5 seconds. Competitors' products which can operate at voltages similar to those for CAP-XX are currently limited to time constants over 1 second. CAP-XX thus has a distinct competitive advantage for applications in which discharge is required in times less than 30 seconds. Other devices will have high losses that will heat and therefore damage the supercapacitor.